Class 6 Maths: Ratio & Proportion Worksheet with Answer Key

Complete ratio and proportion practice sheet for Class 6 students with 24 questions covering cross multiplication, unitary method, inverse proportion, and word problems. Includes detailed solutions and scoring guide.

Understanding Ratio & Proportion

RATIO: A comparison of two quantities of the same kind by division.

Example: If there are 6 boys and 4 girls, the ratio is 6:4 or 3:2 (in simplest form)

Key Points about Ratios:

Same units required: Can't compare 5 kg to 10 grams directly

Order matters: 3:2 ≠ 2:3

Simplify by HCF: 12:18 = 2:3 (divide by 6)

Equivalent ratios: 1:2 = 2:4 = 3:6 = 5:10

PROPORTION: An equation stating that two ratios are equal.

a:b = c:d or a/b = c/d

This means "a is to b as c is to d"

Properties of Proportion:

Product of extremes = Product of means: a × d = b × c

Terms: In a:b = c:d, 'a' and 'd' are extremes, 'b' and 'c' are means

Example: 2:3 = 4:6 → 2×6 = 3×4 → 12 = 12 ✓

Unitary Method:

Finding the value of one unit first, then multiplying.

Example: If 5 pens cost ₹50, find cost of 8 pens

Cost of 1 pen = ₹50 ÷ 5 = ₹10

Cost of 8 pens = ₹10 × 8 = ₹80

Solved Example

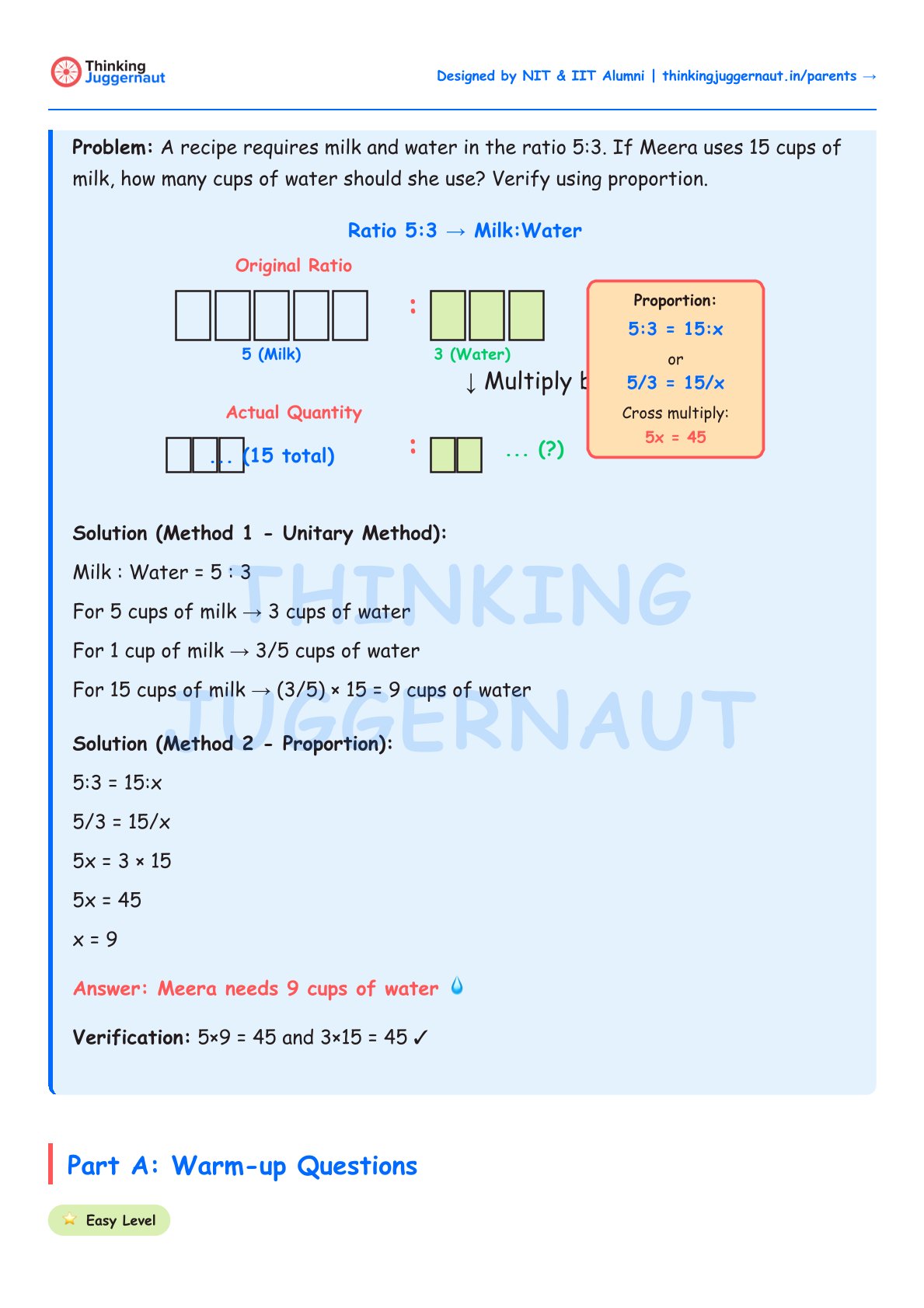
Problem: A recipe requires milk and water in the ratio 5:3. If Meera uses 15 cups of milk, how many cups of water should she use? Verify using proportion.

Solution (Method 1 - Unitary Method):

Milk : Water = 5 : 3

For 5 cups of milk → 3 cups of water

For 1 cup of milk → 3/5 cups of water

For 15 cups of milk → (3/5) × 15 = 9 cups of water

Solution (Method 2 - Proportion):

5:3 = 15:x

5/3 = 15/x

5x = 3 × 15

5x = 45

x = 9

Answer: Meera needs 9 cups of water

Verification: 5×9 = 45 and 3×15 = 45 ✓

Sample Practice Problems

Express the ratio 24:36 in simplest form

Check if the following ratios are in proportion: 3:5 and 6:10

The ratio of boys to girls in a school is 7:5. If there are 280 boys, how many girls are there?

Divide ₹1200 between Ravi and Sita in the ratio 3:5

If 12 workers can complete a task in 8 days, how many days will 16 workers take to complete the same task?

Two numbers are in the ratio 3:5. If 9 is added to each number, the ratio becomes 12:17. Find the numbers.

Scoring Guide

20-24 correct: Excellent! Master level! Practice inverse proportion and compound ratios. Try competitive exam questions.

15-19 correct: Very Good! Strong grasp of concepts. Focus on complex word problems involving multiple ratios.

10-14 correct: Good Effort! Practice cross multiplication and unitary method problems. Review proportion properties.

0-9 correct: Keep Trying! Revise basic concepts. Start with simple ratio problems and equivalent ratios. Practice daily!

Key Concepts to Master

Simplification: Always reduce ratios to simplest form using HCF

Cross Multiplication: In a:b = c:d, remember a×d = b×c

Unitary Method: Find value of ONE unit first, then multiply

Unit Conversion: Convert to same units before comparing (kg to g, hours to minutes)

Total Parts Method: When dividing quantities, add ratio parts to find total

Proportion Check: Product of extremes = Product of means

Common Mistakes to Avoid

Not converting to same units before comparing

Reversing the order of ratio (writing 3:5 instead of 5:3)

Forgetting to simplify the final answer

Adding ratios directly (2:3 + 1:2 ≠ 3:5)

Not verifying proportion using cross multiplication

Confusing direct and inverse proportion